Les élections deviennent vite un vrai casse-tête lorsque l’on parle de proportionnelle. Pourtant ce mode de scrutin est aujourd’hui le plus répandu, il est utilisé notamment pour élire les conseillers municipaux ou encore les sénateurs.
Le scrutin à la proportionnelle a vu le jour avec l’apparition des partis politiques au XIXe siècle. La méthode la plus employée aujourd’hui est celle de la plus forte moyenne. Pour comprendre un peu mieux ce système, focus sur les élections sénatoriales. Celles-ci ont eu lieu en Moselle le 24 septembre dernier. La répartition des sièges se déroule en deux étapes, une partie des sièges est attribuée aux listes grâce au quotient électoral. Les sièges restants seront répartis selon la méthode de la plus forte moyenne.
Première répartition avec le quotient électoral
Pour commencer, les listes ayant obtenues la majorité absolue gagneront automatiquement un siège. Cette majorité se détermine grâce au quotient électoral. Il est calculé par le nombre de suffrages exprimés (nombre de votes émis moins les bulletins blancs et nuls) divisé par le nombre de sièges à pourvoir.
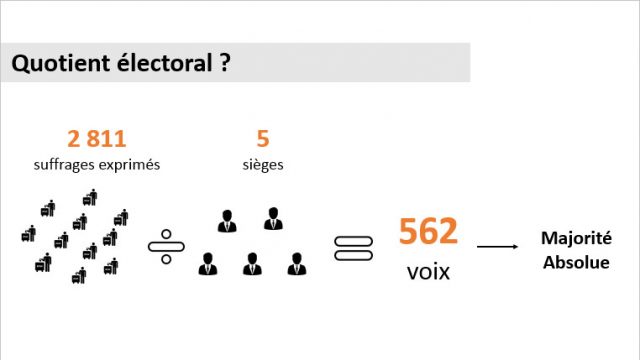
Dans le cas des sénatoriales en Moselle, la majorité absolue s’élevait à 562 voix. Grâce au quotient calculé précédemment, nous allons pouvoir déterminer le nombre de sièges à répartir pour chaque liste. En divisant le nombre de voix obtenues pour chaque parti par le quotient électoral et en le tronquant, on obtient le nombre de sièges. La liste A par exemple a obtenu 640 voix, si on divise ce nombre par le quotient (562 voix), on obtient un résultat de 1,138. Si on le tronque, la liste A gagne 1 siège. Les listes A et B obtiennent donc chacune 1 siège avec cette première répartition.
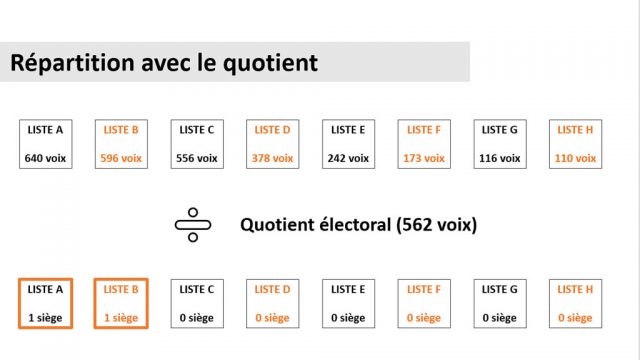
Répartition des sièges restants avec la méthode de la plus forte moyenne
Deux sièges ont déjà été répartis, il en reste donc plus que trois à attribuer. Comment se déroule cette répartition ?
Pour distribuer les trois sièges restants, c’est la méthode de la plus forte moyenne qui prévaut. Elle va s’appliquer à toutes les listes sous la forme d’un algorithme qui peut s’imager par le processus qui va permettre de transformer un grain de blé (la matière brute) en farine (matière finie). Dans notre cas par exemple, le grain de blé correspond au nombre de voix obtenue par chacune des listes. Ce grain de blé va ensuite être ensuite broyé dans un moulin, pour en faire de la farine. Le moulin illustre la suite de calculs que va subir la donnée en entrée. La farine, quant à elle, correspond au score obtenu par chaque liste en sortie. Cette méthode est appliquée en trois étapes, afin d’attribuer les sièges restants.
Par exemple, la liste A a remporté 640 suffrages, si on applique la méthode avec la plus forte moyenne, on divise ceux-ci par le nombre de sièges obtenues à l’étape précédente (un siège) auquel on ajoute 1, on obtient un score de 320. La liste A n’ayant pas obtenu le plus grand score, elle ne remporte aucun siège à cette étape. On répète l’action encore 2 fois.
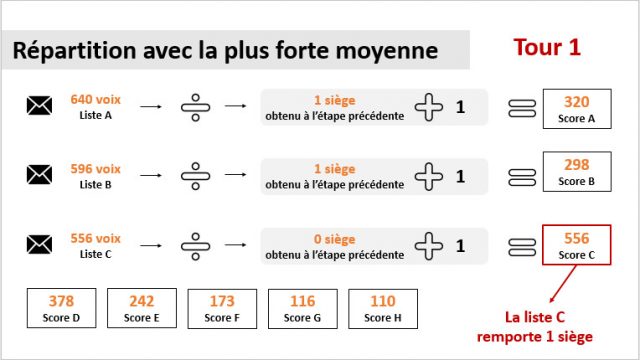
Les 8 listes obtiennent donc un score, celle qui décroche le score le plus élevé acquiert 1 siège. Cette action sera répétée encore 2 fois pour répartir les 2 restants. Au final, la liste A obtiendra au total 2 sièges, et les liste B, C et D un seul.


